IBD Estimation
The objective is to compute the probability of two alleles being shared IBD given the genotype data at that locus and the entire, unbroken pedigree. With very deep pedigrees it is often the case that many generations will have no genotype data, whereas more recent generations do. An efficient implementation will necessarily take this difference in information into account and execute different strategies in the two realms. My approach is based on the same recursive method suggested by Wang et al. (1995) and Davis et al. (1996) and is analogous to the recurrence relation for kinship coefficients,
where 
and 
are the mother and father of 
. The above equation holds as long as 
is not a descendant of 
. The methods of Wang et al. and Davis et al. extend this to the case where there is genotype data,
with the subscripts indicating the particular allele (with arbitrary ordering) of the individual and 
representing the genotype data. Also, the notation 
is used to indicate IBD and 
means “inherited from.” The problem with this approach is that it does not hold true when genotype data are missing.
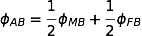
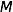
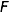
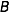
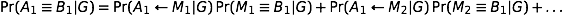
Accounting for missing data correctly is critical to any real-world data analysis. Both Wang et al. and Davis et al. suggest Monte Carlo approaches for dealing with missing data. Unfortunately, this approach can be time consuming. This problem is exacerbated when there are many individuals in the pedigree who are not typed at all, as is often the case with large and deep pedigrees. In such a situation it can be computationally impractical to apply the recurrence relation all the way to the founders.
My method uses a different strategy to these problems, and, in the process, can estimate IBD between pairs of individuals with unprecedented speed. Although I start with the same basic recurrence relation above, I expand the probabilistic framework so that it is exactly applicable even when individuals have missing genotype data. The actual implementation allows for greater speed by applying approximations, but now the results are completely deterministic and do not have any Monte Carlo variability. Also, I rework the boundary conditions for the recurrence relation to apply to a specified set of individuals, the “quasi founders.” The quasi founders are, in general, the oldest set of genotyped individuals, although this is not strictly necessary.
This method can estimate the IBD sharing between 11,026 pairs (every possible pair of 148 individuals) from a 13 generation, 3,028 individual pedigree with 700 people genotyped with an average speed of 0.042 seconds with a highly informative marker. (The marker is modeled as a “haplotype marker” composed of many tightly linked SNPs, as might be obtained from a 100k or 500k SNP chip, with 20 alleles and a heterozygosity of 0.87.) The average speed when the marker is a SNP is 0.14 seconds per marker.
The software can either estimate the IBD sharing for each pair or perform qualitative trait linkage analysis using the 
sharing statistic as described in the paper (not yet published). The software must read in the pedigree, study sample and genotype data files to determine the quasi founders. Once the quasi founders are known, you must use my identity coefficient calculating software (or any software that can compute the condensed identity coefficients, but I don’t actually know of any, feel free to let me know if you do) on the specified set of individuals. Once these have been determined, the program can then go about doing its computations. The program also requires that you either specify a file with allele frequency information or specify that it should estimate the allele frequencies from the data. Unless you have estimates of the allele frequency in the founder population (or a population that you think is reasonably representative of the founder population) it is probably better to let the program estimate the allele frequencies rather than put in your own frequencies, particularly if your frequencies have been estimated from the data you wish to analyze.
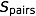
References
Wang T, Fernando R, Vanderbeek S, Grossman M, Vanarendonk J (1995) Covariance between relatives for a marked quantitative trait locus. Genet Sel Evol 27:251–274
Davis S, Schroeder M, Goldin LR, Weeks DE (1996) Nonparametric simulation-based statistics for detecting linkage in general pedigrees. Am J Hum Genet 58:867–880
Updated July 3, 2007