BUILDING A BRIDGE BETWEEN AB INITIO AND SEMIEMPIRICAL
THEORIES OF MOLECULAR ELECTRONIC STRUCTURE
Karl F. Freed
James Franck Institute and Department of Chemistry
The University of Chicago, Chicago, Illinois 60637 USA
To appear in "Conceptual Trends in Quantum Chemistry" 2,
Ed. E. Kryachko and J. L. Calais (Kluwer).
1 Introduction
The phenomenal increase in computer capabilities, new theoretical developments, and advances in algorithms have sparked a likewise phenomenal increase in the capabilities of ab initio electronic structure methods for accurately describing molecular electronic structure. Thus, ab initio electronic structure computer "packages" are now available to the general scientific community, and their usage is in a rapid stage of growth. While there is a concomitant increase in the sizes of molecules that may be accurately treated with ab initio methods, interesting molecular systems always exist that far exceed the capabilities of the most advanced ab initio electronic structure approaches. Consequently, many approximate and semiempirical electronic structure methods are and must always continue to be necessary for describing the electronic properties of these large systems.
The early development of theories for chemical bonding focused upon semiempirical approaches
,, for simple pi-electron systems. Most modern semiempirical approaches are direct generalizations of the earlier successful pi-electron methods. One generic example is Hÿuckel theory for the electronic structure of pi-electron systems. The pi-electron methods form a central position in the history and the development of semiempirical methods1,2. Deficiencies with the predictions of the one-electron Hÿuckel pi-electron methods led to the introduction of Pariser-Parr-Pople (PPP) theory1,, which explicitly contains the electron-electron repulsion. Further developments involve the inclusion of "all" valence electrons. The structures of these newer (and current) semiempirical methods are direct generalizations of the earlier successful pi-electron methods.The advent of digital computers has provided the tools necessary for performing ab initio computations for the smallest of molecules, and these earliest computations already raised serious questions concerning the fundamental assumptions of semiempirical methods, questions which are continually reinforced by comparisons with accurate ab initio computations and which persist even today for the most advanced semiempirical approaches. A review of these questions provides insights and challenges associated with relating ab initio and semiempirical electronic structure approaches. First of all, the most sophisticated semiempirical methods employ a minimal basis set of orbitals, whereas the lowest level of ab initio computations requires at least a split valence orbital basis, twice the valence basis size of that in the all-valence-electron semiempirical approaches. Highly accurate, correlated ab initio computations, on the other hand, require very extensive basis sets with several levels of polarization functions. This glaring difference alone leads many ab initio theorists to question whether the semiempirical approaches are merely sophisticated curve fitting methods, bereft of any true theoretical foundations. Thus, this comparison raises the first and most fundamental question posed by semiempirical methods, namely, whether it is theoretically meaningful to transform the full molecular Schrÿodinger equation with a formally infinite basis set into a valence only problem involving a minimal valence basis
,. (Some frontier orbital methods reduce the valence space further to one or a few highest occupied and lowest unoccupied molecular orbitals).While all electronic structure methods strive for accuracies of one kcal/mol, there are strong differences in how semiempirical and ab initio approaches achieve this goal. The ab initio methods can generate this chemical accuracy only by using large basis sets and high levels of electron correlation, thereby limiting treatment to "smaller" molecules because of the great computational expense. (However, the definition of "small" in this context is constantly growing with time!) Semiempirical methods likewise strive for accuracies of fractions of a kcal/mol for bond and low lying electronic excitation energies of rather large and complex molecules. Their achieved accuracies are about 4kcal/mol for hydrocarbons and less for more complicated molecules
. Nevertheless, the semiempirical approaches accomplish this admirable feat for molecules which are quite large and for which the most advanced, correlated, ab initio methods would be prohibitive. Thus, the accomplishments of semiempirical electronic structure methods pose the following fundamental question: How can the semiempirical methods achieve such accuracy with just a minimal valence basis set? The general rationale argues3 that the valence orbital integrals over one and two-electron interactions in the semiempirical methods (called the semiempirical parameters below) have been adjusted to incorporate correlation effects, thereby obviating the need for using an extended basis and also producing the quoted high accuracies. By assuming that semiempirical parameters implicitly include correlation contributions, many additional questions arise as follows1,9: Is the process theoretically justified? If correlation is introduced into semiempirical parameters using a self-consistent field formulation and then if the semiempirical method uses configuration interaction (CI) in the computation of energies, has there been double counting1,9,10 of correlation contributions? Early semiempirical approaches are parametrized either to compute bond energies or electronic excitation energies, etc., but now advanced methods are attempting to obtain geometries, bond, excitation, ionization, etc., energies from a single semiempirical scheme. CI is increasingly being used,, and the double counting question then looms stronger.These questions are heightened further by the general philosophy behind the current construction of semiempirical methods, a philosophy which is best exemplified by Sadlej: "Let us, therefore, assume that our wavefunctions arise from non-empirical calculations. The resulting assertions and conclusions will then be extended to corresponding semiempirical variants of these methods. How far this procedure is valid can only be justified a posteriori by comparing the results with those arising from non-empirical calculations or with experimental data. Nevertheless, it is commonly accepted that useful theorems valid for non-empirical functions are also valid for semiempirical versions of the same method. Unfavorable theorems and conclusions are eliminated by an appropriate choice of empirical parameters." Thus, the all-valence-electron methods are generally parametrized by considering the form of Hamiltonian matrix elements within a minimal valence orbital basis set
5, but this is done with an underlying hope3 that "correlation contributions" from the complete set of omitted orbitals may somehow be incorporated into the semiempirical parameters.If it were possible to derive exact expressions for correlation contributions to the individual integrals, then a number of the assumptions regarding the structure and transferability of semiempirical parameters could be tested directly
1, thereby hopefully reducing the laborious trial and error process currently required in deriving new parameter sets17. Lacking the theoretical expressions for the correlation contributions to individual integrals, semiempirical parameterizations have proceeded under the assumption that it is merely necessary to alter the form of theoretical integrals to incorporate correlation corrections. This bold assumption requires testing based on rigorous quantum mechanical theories enabling the ab initio computation of all semiempirical parameters1. It is, of course, likely that these sophisticated tests would suggest revision of current practices. Nevertheless, even given the strong assumption of merely modifying theoretical integrals, it has been necessary to proceed by a laborious trial and error parameterization procedure that lengthens as the semiempirical method becomes more sophisticated14,15,17. Thus, a derivation of computationally usable expressions for these individual correlation contributions would enable addressing such a basic question as to whether semiempirical methods are neglecting significant parameters. For instance, the zero differential overlap (ZDO) approximation argues that certain repulsion integrals become small in a Lÿowdin orbital basis and are therefore negligible. However, the theoretical nearest-neighbor, two-center, pi-electron exchange integral for carbon atoms is about 0.3eV and is quite significant for methods that strive towards accuracies of less than a kcal/mol. Does the inclusion of correlation make this parameter small enough to be truly negligible, or does correlation enhance its value to the extent that its retention is warranted in semiempirical methods? Similar arguments apply to other ZDO approximation neglected interactions. The question has numerous applications as Hirsch has argued that a two-electron contribution to resonance integrals is necessary for understanding the electronic structure of high temperature superconductors, while Iwata and Freed have shown how the same interaction contributes, in part, to the breakdown of the paring theorem in alternant hydrocarbons, leading, for example, to a dissymmetry between the spectra of cations and anions.Several fundamental questions center on whether other parameters exhibit correlation contributions with different dependences on bond lengths, etc., than assumed in semiempirical models because the prior parameterizations have proceeded without the benefit of rigorous, systematic, ab initio theoretical guidance concerning the structure of correlation contributions to individual parameters. Some semiempirical practitioners already appreciate
14 the role of theory in formulating improved semiempirical approaches: "æææ parameterization based only on experimental results can lead to strange physical behavior in regions where no or a small number of experimental data are available. Ab initio calculations may help fix those problems." Thus, resolving some of the questions posed above could have several beneficial consequences. The first is that ab initio theoretical descriptions of parameter dependences must be richer and more accurate than the more intuitive ones currently in use. Additional parameters may be necessary, and alternative variations with bond lengths may be uncovered.Ab initio theory may aid in further extending the capabilities of current semiempirical methods. These extensions include alleviating present difficulties in parameterizing semiempirical methods with extended valence spaces. Completely satisfactory parameterizations are still lacking for transition metal systems, especially if the desire is to obtain semiempirical methods that cover the whole range of formal charge states, high and low spin, and bond as well as electronic excitation energies. Extensions would be welcomed to computations of the parameters in semiempirical treatments of solids, especially high temperature superconductors, conducting polymers, and nonlinear optical materials. Furthermore, semiempirical methods are notoriously poor in representing dipole moments of small molecules, while they are extensively used for describing nonlinear optical properties of large molecules. The same semiempirical methods are parametrized to describe the energetics of small molecules
12,14,15,17,,, before using them for larger systems, so the difficulties with treating dipole moments of small molecules signals the presence in semiempirical methods of serious systematic errors whose resolution with theoretical guidance must have important practical ramifications.While theory might contribute to many possible improvements of semiempirical methods, a more thorough understanding of the latter may enhance purely ab initio capabilities. Semiempirical methods are predicated on the use of localized, transferable parameters, and the successes of semiempirical methods suggest that correlation can indeed be represented in a localized fashion, a form in which many ab initio theories have sought to express correlation for more efficient computation in large molecular systems. A more thorough understanding of how correlation enters into individual semiempirical parameters may therefore aid with the development of localized ab initio correlation treatments.
The first and most fundamental question in devising practical theoretical connections between ab initio and semiempirical approaches lies in explaining whether and why the full Schrÿodinger equation can be transformed to a minimal valence shell problem with perhaps some different structure than that customarily assumed by semiempirical methods
9,10,. Thus, section II considers the establishment of this formal bridge, followed by section III in which we outline recent ab initio computations based upon the resultant theoretical formulation, computations which assess the possible accuracy of calculating the correlation contributions to individual parameters. This section indicates the requisite high degree of correlation, the large basis sets, and hence the huge scale computations, which have only recently become possible to the degree necessary for treating interesting molecular systems. Section IV describes recent advances in calculating the correlation contributions to individual parameters.
2. Theoretical bridge between ab initioand semiempirical methods
We confine attention to those semiempirical methods that are characterized by using a set of valence orbitals and a semiempirical effective valence shell Hamiltonian H
Mv, which contains the empirical parameters. Thus, our considerations do not include density functional or many-body Green's function approaches, which necessitate the use of different theoretical formulations. Early attempts at a theoretical justification of semiempirical methods1 are flawed because most are based on overly optimistic beliefs concerning the type of ab initio computation that is necessary to achieve experimental accuracy. Many more recent attempts focus narrowly on oversimplified models as discussed below. Thus, we begin by assessing what are the components of semiempirical methods that may be tested theoretically.An optimal semiempirical method enables accurate computation of bond energies, activation barriers to chemical reactions, electronic excitation energies, ionization potentials, etc., with a single set of parameters for all properties and electronic states of interest. Consequently, this optimal many-state approach cannot be understood with widely used theoretical "justifications" of semiempirical models that are based on the properties of only a single electronic state (usually the ground state). These single state arguments generally begin with the expression for the self-consistent field (SCF) energy and then append pairwise additive correlation energies. The many-state H
Mv must be understood with a more sophisticated theory involving many electronic states of a given molecular system.
2.1. DERIVATION OF THE EXACT EFFECTIVE VALENCE SHELL ONLY EQUATIONS
The many-state analog of H
Mv may simply be determined by analyzing the logical (i.e., purely mathematical) content of this HMv. Given a particular HMv along with its set of valence orbitals, it is, in principle, possible to solve for all its eigenfunctions ˆiv and eigenvalues Ei by expanding the semiempirical wavefunction ˆiv in terms of the valence functions |pê, where |pê is, for instance, a determinantal function containing electrons only in the valence orbitals (with a filled core implicit)9,10,30. Thus, we have the semiempirical Schrÿodinger equation,Hˆ= E
iˆ, (2.1)where ˆis given by the full valence shell CI expansion.
ˆ= C
pi|pê. (2.2)
Combining equations (2.1) and (2.2) and using standard matrix notation converts these into
HC
i = EiCi. (2.3)When applying the semiempirical methods to large molecular systems, it is often desirable to approximate the ˆ
iv using less than a full valence shell CI computation, but the introduction of this numerical approximation represents a secondary question that may be addressed subsequently. (It is well understood that the choice of semiempirical parameters depends somewhat on the amount of CI that is used in conjunction with the method.) We, therefore, seek to determine whether the full electronic Schrÿodinger equation,Hˆ
i = Eiˆi, (2.4)can be expressed equivalently in a valence only representation of the form in Eq. (2.3), but with an exact effective valence shell Hamiltonian matrix H
v replacing the semiempirical model HMv in Eq. (2.3) and with Ei in Eq. (2.3) identical to the exact energy in (2.4).The formal derivation of this exact effective valence shell Hamiltonian is quite straightforward
9,10,30,,. Let |pê also designate the zeroth order valence space wavefunction with the filled core orbitals explicitly included. Now collect the full Hamiltonian H matrix elements âp|H|p'ê between the valence configurations |pê and |p'ê into the block matrix HPP, where the subscript P designates the valence space. An exact ab initio computation requires the introduction of a set (in principle, infinite) of complimentary configurations {|qê} which contain occupied excited orbitals, vacant core orbitals, or both. The Hamiltonian matrix âq|H|q'ê in the "excited" (or "correlating") space is likewise collected into the block matrix HQQ. Introducing the off-diagonal blocks between P and Q-spaces as HPQ and HQP and the P and Q-space blocks of the CI column vectors CiP and CiQ, respectively, equations (2.4) with the full CI analog of Eq. (2.2) are transformed into the block matrix equations,= E , (2.5)
where the state index i has been dropped for convenience. Multiplying out the block matrix equations from Eq. (2.5) yields the pair of matrix equations
H
PPCP + HPQCQ = ECP, (2.6a)H
QPCP + HQQCQ = ECQ. (2.6b)Formally solving equation (2.6b) as
C
Q = (E1Q - HQQ)Ä¡HQPCP (2.6c)enables the substitution of Eq. (2.6c) into (2.6a) to give the exact effective valence shell Schrÿodinger equation as
H
vCP = ECP, (2.7)where the exact effective valence shell Hamiltonian is obtained as
H
v = HPP + HPQ(E1Q - HQQ)Ä¡HQP. (2.8)Equation (2.8) is a matrix solely in the space of valence functions. However, the correlation corrections enter into Eq. (2.8) from the remainder of the infinite (complete) basis set
Equation (2.7) has the identical formal structure as the semiempirical full CI equations (2.3) when it is recognized
9,10,30 that the two basis sets involve formally identical sets of valence functions |pê. Thus, the full semiempirical matrix Schrÿodinger equation (2.3) represents an attempt to mimic the exact matrix equation (2.7). Consequently, the above simple derivation proves that it is meaningful to reduce the full electronic Schrÿodinger equation to a valence orbital only equation, provided the Hamiltonian in this valence space is taken as the exact effective valence shell Hamiltonian Hv of (2.8). The valence orbital basis may be a minimal basis, or it may contain fewer frontier orbitals. The exact Hv is, however, different for these two choices of valence spaces.Although equations (2.7) and (2.8) justify the first and most fundamental minimal basis tenet of semiempirical methods, there is no guarantee yet that the exact H
v of (2.8) has almost the precise structure postulated by some semiempirical methods. First of all, the explicit dependence of Eq. (2.8) on the state energy E differs from the assumed semiempirical forms. The next subsection, however, introduces expansions which remove this E-dependence to produce computationally viable expressions for Hv that are independent of E and therefore identical for all states of interest. Thus, we now turn to an examination of some properties of and some computational procedures for Hv.2.2. PROPERTIES OF AND COMPUTATIONAL METHODS FOR Hv
The first H
PP contribution to Hv in Eq. (2.8) is just the Hamiltonian matrix in the space of valence functions, while the second term on the right hand side of Eq. (2.8) represents the "correlation contribution" because it involves excitations into a complete set of excited orbitals, excitations out of the core orbitals, and all possible combinations of both. The matrix elements in HPP contain the "theoretical" or "bare" integrals, while the correlation contribution exactly adjusts all these integrals for correlation as implicitly assumed by the semiempirical methods. Many ab initio theorists mistakenly believe that the semiempirical methods approximate HPP alone, but the formal derivation of Eq. (2.8) proves that it is possible to incorporate all correlation contributions into the valence only problem of Eq. (2.7).Unfortunately, the exact computation of H
v from Eq. (2.8) is impossible because the inverse matrix is infinite, and the use of large basis sets renders the matrix much too huge to be inverted for large systems. Thus, some approximations are necessary beyond the well-studied ones of using finite basis sets. One convenient approach to computing the Hv of Eq. (2.8) involves the introduction of many-state (van Vleck type,,,) Rayleigh-Schrÿodinger perturbation theory. As now described, these formulations produce perturbative expressions for an approximate Hv which no longer depends on the individual states, e.g., as does Eq. (2.8) by virtue of the presence in the denominator of the unknown state energy E.For convenience, we present the perturbation theory formulas for the case in which the valence space is taken to be exactly degenerate. The application of perturbation theory requires the decomposition of the full Hamiltonian H into its zeroth order part H‚ and the perturbation V,
H = H‚ + V, (2.9)
where the valence space determinantal functions |pê and the secondary space determinantal functions |qê are eigenfunctions of H‚,
H‚|pê = E
pº|pê, H‚|qê = Eqº|qê. (2.10)The condition of complete degeneracy is that E
pº = EPº for all |pê in the valence space. The exact energies E in the denominator or Eq. (2.8) must likewise be expanded about the zeroth order energies EPº, and a wide variety of formalisms exist for accomplishing this expansion,,. (The details are somewhat more involved for the non-degenerate case.) Degeneracy simplifies the multireference perturbation expression for the Hermitian Hv intoâp|Hv|p'ê = âp|H|p'ê +
+ +
+ h.c. + æææ, (2.11)
where h.c. designates the Hermitian conjugate of the preceding term.
The individual third order contributions to Eq. (2.11) [ containing the sums over q,q' and q,p'', respectively] have portions incorrectly scaling as the square of the number of electrons in the system. Brandow
39, however, has shown that upon use of a "complete" valence space (see the definition below), the improper terms cancel identically between these two third order terms and the combination of these two third order contributions is indeed size-extensive, scaling properly with the number of electrons in the system. Brandow's linked-cluster theorem is proven to all orders in multireference configuration perturbation theory39, and Brandow presents a convenient diagrammatic method34,39 for reducing the original perturbation expressions, which contain N-body matrix elements of V as in Eq. (2.11), to ones in terms of the matrix elements of the one and two-electron interactions in the Hamiltonian within a complete set of core {c}, valence {v} and excited {e} orbitals. The complete valence space requires that the set of valence functions {|pê} represents what is often called a "complete active space" in which the core orbitals are all doubly occupied and the remaining electrons occupy only valence orbitals. However, this complete active space is just that required to make Hv and the semiempirical HMv act on identical spaces9,10,30.The expansion in Eq. (2.11) exhibits each N-electron matrix element âp|H|p'ê as being modified by the correlation contributions which first enter at second order in V. Simple arguments enable showing how this, in turn, implies that the individual matrix elements of the one and two-body portions of H
v contain correlation contributions, thereby formally justifying the alternation of bare H matrix elements for correlation. The actual computation of these matrix elements from Eq. (2.11) is rather involved and is facilitated by use of many-body theory techniques34,39. Since the latter would take us too far afield, we briefly provide a motivational sketch of a possible (but more tedious) procedure that avoids introducing many-body theory.The first tedious step involves substituting N-electron Slater determinants for the functions |pê and |qê into Eq. (2.11) in order to reduce the sums-over-states expressions into ones involving sums over core, valence, and excited orbitals and their matrix elements of the one and two-body interactions in the original Hamiltonian H. When the system contains no valence electrons, Eq. (2.11) provides the nondegenerate perturbation expression for the correlated core energy Ec. Next, we choose the N=1 one-valence-electron states and substitute these N=1 states into the sums-over-states perturbation equations. Then, represent each matrix element in the matrix âp|Hv|p'ê, on the one hand, as an expansion in terms of sums over orbitals. On the other hand, use of the operator representation
Hv = Ec + H,
with H
Mv an effective one-body operator, enables expressing the matrix elements âp|Hv|p'ê as matrix elements of Hiv in the valence orbital basis. Equating the two matrices provides explicit perturbative formulas for computing the valence shell matrix elements âv|Hiv|v'ê, where |vê and |v'ê are valence orbitals.Passing on to the N=2 two-valence-electron states, the matrix elements from the right hand side of Eq. (2.11) in the sum over orbitals form is then equated to the matrix elements constructed from the left hand side using the operator representation
H
v = Ec + H+ H
where H
ijv is the effective two-body operator and the effective one-body operator is that already obtained from the N=1 states. This produces perturbation expansions for the two-electron matrix elements âvŽv¤|Hijv|v‹v›ê, with valence orbitals |vŽê through |v›ê.Let us now analyze in detail one correction term arising from the second order portion of Eq. (2.11) in order to provide further understanding of some general structure of H
v. Consider the contributions from excited configurations |qê containing a single v ü e valence to excited orbital excitation. After evaluation of the N-electron matrix elements, these single excitations yield contributions with the numerator,âvŽv¤||v‹eêâv›e||vÞvþê, (2.12)
where 1/rŽ¤ is the electron-electron interaction in atomic units, vŽ through vþ designate valence orbitals, while e is an excited orbital. The contribution in Eq. (2.12) may, in principle, have all six valence orbitals vŽ,æææ,vþ all different, thereby providing a matrix element of H
v that is off-diagonal in three spin-orbital indices. Such a term can only be represented as part of a three-body effective interaction H123v. Similar analysis demonstrates that the third order terms in Eq. (2.11) yield four-body effective operators H1234v, etc. The true Hv, therefore, has the general structure of9,10,30,
Hv = Ec + H+
H+ H+ æææ, (2.13)
where N
v is the number of valence electrons, Ec is the fully correlated core energy, and Hiv, Hijv, Hijkv, are the one, two, and three-body effective valence shell operators that act only on the space of the valence shell orbitals. The correlation contributions to Eqs. (2.8) and (2.11) imply that, for instance, the individual matrix elements of the effective operator H12v may be written as the sum of the bare (often called theoretical) matrix element âvŽv¤|rŽ¤Ä¡|v‹v›ê plus the correlation portion,âvŽv¤|H|v‹v›ê = âvŽv¤||v‹v›ê + âvŽv¤|
Î|v‹v›ê. (2.14)The process of extracting the correlation contributions like Î
12v from Eq. (2.11) is greatly facilitated by use of many-body techniques, such as those of Iwata and Freed43 or more generally of Brandow's diagrammatic methods34,39,40.The many-body operators in Eq. (2.13) are part of the price paid in order that the H
v of Eqs. (2.8) and (2.11) be exact. The existence in Hv of these non-classical many-body operators is but one indication that the true Hv differs from the forms commonly assumed by semiempirical methods since the latter do not explicitly contain objects such as the three-electron interactions with valence shell matrix elements âvŽv‹v‹|H123v|v›vÞvþê. Consequently, insight into the structure of the true Hv can only emerge from ab initio computations using Eq. (2.11) since no other ab initio formulation is currently available that can compute individual matrix elements of the correlation contributions to H1v, H12v, H123v, æææ. However, before using ab initio methods to compute these correlation corrections, it remains to be determined whether this ab initio effective valence shell Hamiltonian formulation is of suitable ab initio accuracy to warrant drawing conclusions concerning the true Hv from such computations.3. The ab initio H
v methodThere is rather wide spread usage of ordinary non-degenerate Rayleigh-Schrÿodinger perturbation theory, which is termed either many-body perturbation theory or MP theory in the literature. (The "many-body" label is usually applied when the method employs techniques of second quantization and Feynman diagrams, while the MP designation also implies a more restrictive choice of zeroth order orbitals and orbital energies than that desirable for multireference configuration studies.) These non-degenerate methods require a zeroth order description that involves a single determinantal wave function, and most common schemes proceed in an order-by-order fashion, e.g., MPi refers to computations through ith order. Applications are generally restricted to i < 4, and the necessary computer codes are contained in commercially available electronic structure computer packages.
Deficiencies of this non-degenerate perturbation approach are quite obvious when considering developments with the variationally based configuration interaction (CI) methods, which likewise began with treatments based on a single reference configuration. Both single reference CI and perturbation methods encounter difficulties in treating inherently open-shell systems
7,, such as those arising with the ground states of some radicals, many excited electronic states, transition states for chemical reactions, etc. Thus, just as CI methods have been extended7, it is quite natural that the perturbation theory formulations likewise be extended to methods involving many reference configurations.The available multireference configuration CI computations provide some guidance as to requirements of the multiconfigurational perturbation approaches as follows: The multireference CI calculations appear to work quite well, provided that the reference space (the P-space of Sect. 2) contains all of the dominant configurations and provided that the single and double excitations out of these configurations are included in the secondary space (the Q-space of Sect. 2). However, these types of CI methods are formally not size-extensive and, therefore, do not scale properly with the number of electrons in the molecule. Davidson corrections are generally appended to correct for lack of size-extensivity, producing what has been the most viable ab initio method for computing global potential energy surfaces covering wide ranges of geometries. However, when there are several important configurations, the Davidson corrections are no so obviously determined. Multiconfigurational perturbation methods, on the other hand, are inherently size-extensive provided they employ a complete reference space as described in Sect. 2. Experience with multireference configuration CI methods further suggests the need in the analogous perturbation approaches for using sufficient numbers of reference configurations to incorporate all the important configurations for the states of interest.
The use of large reference spaces in perturbation methods, however, would appear to introduce serious difficulties. For instance, the first multireference configuration perturbation calculations for molecules are those of Kaldor for excited states of the H¤ and BH molecules. Kaldor only considers the apparently simplest cases in which there are two electrons occupying two nearly degenerate spatial orbitals ƒ and ˆ, and he applies the Brandow
39 formulation of quasidegenerate many-body perturbation theory to this system. The (complete active space) Brandow theory requires the use of a four (spatial) configuration reference space for the two active electrons, a reference space containing the configurations ƒˆ, ˆƒ, ƒƒ, and ˆˆ. However, Kaldor finds it necessary to restrict the computations to include only the pair of nearly degenerate ƒˆ and ˆƒ configurations because the remaining ƒƒ and ˆˆ configurations are very different in energy from the quasidegenerate pair ƒˆ and ˆƒ. Thus, the inclusion of the ƒƒ and ˆˆ configurations in the reference space would severely violate the quasidegenerate constraints on the Brandow complete reference space formulation of multiconfigurational perturbation theory and would therefore produce erroneous results.Kaldor's calculations demonstrate the precarious nature of complete reference space perturbation computations for the simplest possible case of a two-orbital, two-electron valence space. However, the situation must become even less quasidegenerate and consequently more problematic as the number of spatial valence orbitals (and the number of valence electrons) is increased further to be consistent with the corresponding demands of multireference configuration CI calculations. In fact, it is this inherent difficulty with complete reference space computations that led Kaldor and Hose to develop incomplete reference space formulations of many-body perturbation theory in which the reference space only contains the important quasidegenerate configurations, suggesting that these methods are useful solely in rather limited situations of strict or near degeneracy with no other important reference configurations of very differing zeroth order energies.
Various model problems have been studied to ascertain the convergence properties of quasidegenerate perturbation theory. Simple three-level model computations
, indicate that these perturbation expansions may in some instances converge to the wrong eigenvalue. This may occur when there is an eigenvalue of the matrix HQQ that lies close to a desired reference (P) space eigenvalue. The perturbation expansion may converge to the offending Q-space state, called an intruder state, instead of the desired one in the reference space. Unfortunately, the possible occurrence of intruder state problems has led to the wide spread belief that these problems always occur, despite many useful examples to the contrary33,. Nevertheless, the above considerations indicate the fundamental difficulties associated with developing an accurate ab initio formulation of complete active space multiconfigurational perturbation theory, especially with the large valence spaces that are required for comparisons with semiempirical methods. The simplest examples are provided by atoms,, whose study suffices for attempting to understand the correct choice of one-center integrals for semiempirical methods.,, First row atoms have a valence space which contains the 2s and 2p orbitals. However, the 2s-2p energy separation grows considerable in crossing the first row, making it highly unlikely that these systems satisfy the quasidegeneracy criterion required for use of the Brandow formulation or variants thereof. Matters become much worse when studying transition metal atoms54 or diatomic molecules involving a pair of first row atoms,,. The latter case has eight spatial valence orbitals, leading to zeroth order valence space configurations with an energy span that may exceed the ionization potentials and that is, therefore, by no stretch of the imagination quasidegenerate!2.1. DESCRIPTION OF THE AB INITIO H
v METHODBecause an understanding of semiempirical methods requires the use of a complete active space formulation of multiconfigurational reference perturbation theory, the corresponding ab initio method must treat rather large, manifestly not quasidegenerate valence spaces. This formidable problem has been handled by simply using a zeroth order Hamiltonian H‚ that forces the zeroth order valence space states to be exactly degenerate, leaving the considerable spread in original valence space energies as a large perturbation that enters into the theory only beginning in third order
34. When the valence space contains four or more electrons, the third order quasidegenerate many-body perturbation theory requires the evaluation of several hundred diagrams and represents an enormous and complicated computational task. These third order corrections are necessary in order to assure that the large perturbation, emerging from the actual spread of zeroth order valence space energies, does not cause any practical difficulties with the theory.Just as an optimal semiempirical method produces all energies using a single minimal basis and a single H
Mv with the same atomic orbital basis "integrals" for all states, the diagonalization of the effective valence shell Hamiltonian Hv, in principle, generates all valence (P-space) state energies simultaneously from a single computation. The orbitals in the Hv method obviously involve appropriate linear combinations of the original basis functions, but somehow the perturbation contributions in Eq. (2.11) are correcting the effective valence shell Hamiltonian Hv for the differences in orbitals that are optimal for individual states as in SCF or MCSCF computations.There is therefore a sharp contrast between traditional wavefunction methods, which employ bare Hamiltonian matrix elements and different orbitals for each state, and the H
v method which has correlation modified effective matrix elements and the same orbitals for all states. This sharp contrast, resembles one that is well known for the different representations of the time-dependent Schrÿodinger equation. A discussion of this analogy further aids in understanding the operation of the Hv method and therefore of semiempirical electronic structure methods. Traditional SCF, CI, etc., wavefunction methods optimize a set of orbitals for each state separately and then use these orbitals to compute correlation corrections. This whole process is carried out with the original, bare Hamiltonian H, much as the Schrÿodinger picture of time-dependent quantum mechanics has the states change with time and the operators remain the same. On the other hand, the Hv method corresponds more closely to the Heisenberg picture of time-dependent quantum mechanics in which the states remain the same, while the operators change with time. This situation corresponds to the Hv method where the orbitals are the same for all states, but the Hv operator changes to describe the different orbital polarizations, etc., between the different valence states.Semiempirical methods implicitly assume that this single-orbital, single-H
Mv procedure is well defined. The ability of the ab initio Hv method to generate many states simultaneously from the diagonalization of a single Hv operator would provide justification for this bold semiempirical assumption as normal intuition, based upon traditional ab initio computations, suggests that this should not be possible. The ability to use a common set of orbitals in the ab initio Hv method, on the other hand, would be beneficial in computations of off-diagonal electronic matrix elements (transition dipoles28, spin-orbit and derivative couplings, etc.) since the use of different and therefore nonorthogonal orbitals in traditional wavefunction methods complicates the computation of these transition matrix elements.The effective valence shell Hamiltonian method is completely specified once choices have been made of a) normalization, b) order of truncation of the perturbation expansion, c) the valence space, d) the orbitals (core, valence, and excited), and e) the zeroth order Hamiltonian H‚. We choose to work only with the Hermitian form of H
v and to retain all contributions through third order. The Hermitian form is natural for comparison with semiempirical HMv, while the use of large valence spaces with more than two valence electrons precludes treating higher than third order. Perhaps, there exist useful partial summations to all orders of certain contributions34, and further analysis of this possibility would be desirable. Hence, the only real freedom in the Hv method is associated with choosing c) through e) above.In performing comparisons of the ab initio H
v method with semiempirical approaches, a natural choice of valence space is the one taken for the corresponding semiempirical method. Semiempirical computations for large molecules involve the use of very large valence spaces, which are currently impractical for Hv computations. However, highly correlated ab initio methods are most suitable for describing smaller molecules. Furthermore, a sufficient test of the assumptions inherent in semiempirical methods requires only the treatment of smaller molecules because the semiempirical methods assume that only one and two-center integrals (or parameters) are present. Thus, the simplest tests of one-center integrals necessitates computations for atoms52-59, while the analysis of semiempirical two-center integrals may be accomplished based on ab initio Hv computations for diatomic molecules. More interesting tests of the transferability assumption of semiempirical methods, on the other hand, require consideration of small polyatomic molecules,. Our desire is to apply the Hv method to molecules of similar sizes to those treated by the other most advanced correlated electronic structure methods. Many of these cases lead to rather large valence spaces of the all-valence-electron variety, thereby raising questions concerning the optimal choice of valence spaces. However, the initial Hv studies consider systems for which the valence space may readily be taken as identical to that of the corresponding semiempirical approach. The orbitals, however, must somehow be optimized for maximal ab initio accuracy and, therefore, must differ in precise form from the (actually often partially unspecified) orbitals in the semiempirical methods.The leading, first order approximation in the Hv method is provided by the full valence shell CI computation produced by diagonalizing the matrix H
PP of Eq. (2.8). Thus, we minimize the perturbation corrections in equation (2.11) and thereby facilitate the convergence of the perturbation expansion by having HPP provide an optimal description for all the valence states since all of their energies, in principle, emerge from a single Hv. Consequently, in principle, the valence space, and hence the core and valence orbitals, might be chosen from natural orbitals or from some systematic averaged complete active space self-consistent field (CASSCF) formulation for all valence states. However, it is rather unrealistic to expect the Hv method to provide a meaningful description of the high lying states in large valence spaces, and this suggests limiting the orbital optimization to a group of lower lying states, which, in general are the states of interest in both ab initio and semiempirical applications. The CASSSCF orbitals for a single state contain some low occupancy valence orbitals that are useful for correlating that state but that are rather poor for describing other excited states in which this orbital is occupied. Lacking the ability to perform state averaged CASSCF computations with states of differing symmetries, the Hv computations have primarily chosen valence orbitals from a sequence of SCF computations for several low lying states as providing a reasonable compromise designed to "optimize" the description afforded by HPP for the low lying states of interest. Other choices involving CASSCF orbitals are currently being tested.We illustrate this choice of valence orbitals by the example of the pi-electron states of trans-butadiene. The semiempirical pi-electron Hamiltonians describe the pi-electron states of this molecule with a basis of four localized atomic-like p¼ orbitals
1, and, consequently, the ab initio Hv method naturally should begin with a set of four "optimized" pi-electron molecular orbitals. The core sigma and valence pi-orbitals have been obtained from the following sequence of single state SCF computations65:(1) (core)(1¼
u)™(1¼g)™, ¡Ag,(2) [(core)(1¼
u)™(1¼g)¡](2¼u)¡, £Bu,(3) [(core)(1¼
u)™(1¼g)¡(2¼u)º](2¼g)¡, £Ag,(4) [(core)(1¼
u)™(1¼g)™(2¼u)º(2¼g)º], ¡Ag, (3.1)where (core) designates a filled sigma core. Step (1) is just a SCF computation for the trans-butadiene ground state, and this calculation serves to define the core and the 1¼
u and 1¼g valence orbitals. The next step (2) is a £Bu state SCF computation in which the core and 1¼u and 1¼g valence orbitals are frozen to be the orbitals generated from step (1), while only the 2¼u orbital is varied. Frozen orbitals are placed inside square brackets, and only those orbitals outside the square brackets are permitted to vary in each step. Because step (2) involves variation of only the 2¼u orbital, this step corresponds to the computation of an improved virtual orbital (IVO), which is "optimal" for the £Bu state given the already obtained ground state orbitals. Although the £Bu state is an electronically excited state, the IVO computation is equivalent to that for a simple ground state. Step (3) continues this practice in computing an IVO for the 2¼g orbital, while step (4) freezes all core and excited orbitals to obtain the virtual orbitals from a ground ¡Ag state computation. Because step (4) employs a ground state Fock operator, the virtual orbitals are determined in the field of the N core and valence electrons for reasons discussed below in conjunction with a description of the choice of zeroth order Hamiltonian H‚. The sequence of SCF computations produces orbitals that are better suited to the ground and lowest excited states. Thus, several other choices of orbitals have been tested and are currently under investigation64, but the above scheme works about the best (of several tried65) for describing all the low lying pi-electron states simultaneously. Nevertheless, some computations in progress for larger conjugated systems find that the highest lying IVO's from this sequential scheme develops too much Rydberg character. Thus, there is a still need for further improvement of the above scheme for choosing valence orbitals.The only remaining ingredient requiring specification in the H
v method is the zeroth order Hamiltonian H‚. The most common choices for perturbation methods involve taking H‚ to be a sum of one-electron operators hŽ, which are individually diagonal among the set of core {|cê}, valence {|vê}, and excited {|eê} orbitals. The Moller-Plesset partitioning, for instance, considers hŽ to be a ground state Fock operator, while MCSCF theories provide several alternative multiconfigurational Fock operators. However, the most general form for this one-electron hŽ may be written in the form,hŽ = ´
c|cêâc| + ´v|vêâv| + ´e|eêâe|, (3.2)
where the diagonal one-electron "orbital energies" {´
c,´v,´e} are, in principle, arbitrary. The first order theory is obtained from the valence block HPP of the full Hamiltonian and, therefore, is independent of the choice of hŽ. Thus, hŽ should be chosen as somehow optimizing the performance of the perturbation expansion. Hence, there is no reason to expect that an "optimal' approach is necessarily provided by the traditional choices for Moller-Plesset single configuration nondegenerate perturbation theory. By analogy with nondegenerate perturbation methods, a natural first choice involves defining the orbital energies as those emerging from the SCF, MCSCF, or CASSCF equations used to compute the corresponding orbitals. The sequential SCF approach, illustrated by Eq. (3.1), employs different Fock operators to obtain the valence orbitals that are unoccupied in the ground state SCF wavefunction.Although the H
v method admits of very general forms for the zeroth order hŽ in Eq. (3.2), a poor choice of orbital energies can doom to failure the perturbation expansion, even through third order. It is possible, however, to understand the stringent restrictions34 on the orbitals and orbital energies by examining the energy denominators appearing in the sums-over-orbitals representation of the perturbation expansion for Hv. Some of the second order contributions to matrix elements of the two and three-electron effective operators H12v and H123v contain energy denominators of the form34,52denominator = ´
v - ´e + ´v' - ´v'', (3.3)where v, v', and v'' refer to valence shell spin-orbitals, and e is an excited orbital. (Similar denominators appear with ´
v - ´e replaced by ´c - ´v, where ´c is a core orbital energy.) The contribution ´v - ´e is always positive (as is ´c - ´v), so long as we make the natural choice of all valence orbital energies lower than those in the excited space (and higher than those in the core). However, when the valence space is not degenerate, the other contribution ´v' - ´v'' may be of either sign. Thus, if the minimum valence to excited orbital excitation energy min|´v - ´e| is equal to the spread in valence orbital energies max|´v' - ´v''|, the denominator in Eq. (3.3) may diverge34, and the perturbation expansion becomes ill-defined already in second order. Experience with second order Hv computations suggests the quasidegenerate condition34min{|´
v - ´e|,|´c - ´v|} > 2 max|´v' - ´v''| (3.4)to assure proper behavior of the second order treatment. However, we have already explained the necessity for using large valence spaces to produce accurate ab initio computations and, of course, for comparison with semiempirical methods. Large valence spaces yield large spreads in valence orbital energies (for any reasonable choice of orbital energies) and thereby rapidly violate the quasidegenerate conditions in Eq. (3.4). The situation becomes even more problematic in third order where some denominators contain two contributions of the form ´
v' - ´v''. Computational experience34 shows that these terms are well behaved provided that the factor of 2 on the right hand side of Eq. (3.4) is replaced by a factor of 3. The more stringent quasidegenerate constraint of Eq. (3.4) with the factor of 3 is met by first row atoms with (four orbital) valence spaces composed of their 2s and 2p orbitals, but already fails for the five orbital valence space description of first row diatomic hydrides. (Some illustrative examples are given below.) Several model analyses of quasidegenerate perturbation methods have obtained divergent behavior because the orbital energies employed severely violate the quasidegenerate constraint49.The above examples illustrate the predicament that the quasidegeneracy constraint appears to preclude the use of large valence spaces. In order to avoid the appearance of small energy denominators in the H
v perturbation expansions for large, non-degenerate valence spaces, the valence orbital energies in HŽ of Eq. (3.2) may be shifted closer together without sacrificing ab initio rigor. While this may at first sight appear to be artificial in comparison with nondegenerate perturbation methods which naturally employ, for instance, SCF orbital energies in H‚, the completely general definition of hŽ in Eq. (3.2) admits, in principle, of any choice for the orbital energies. Of course, a poor choice may lead to the divergence of the perturbation expansion in Eq. (2.11). Thus, an analysis of the perturbation expansion provides the only means for assessing the relative merits for various definitions of hŽ. Reducing the valence orbital energy spread to satisfy Eq. (3.4) with a factor of 3, replacing the factor of 2 on the right hand side of this equation, serves to eliminate the numerator problems, but then it introduces into the perturbation V (and, hence, into the denominators of the perturbation expansion) correction terms containing the shift in the orbital energies. These correction terms first contribute in third order, and, therefore, we have chosen to regularly perform third order Hv computations to assure that the shifts introduce none of the above denominator problems and that indeed the changes in state energies between second and third orders are considerably smaller than those between first and second orders. The latter is a reasonable definition of practical convergence of the Hv method through third order, so long as there is good agreement with benchmark full CI computations62,64, and with experiment when large basis sets are used65.The above described denominator problems are completely eliminated by forcing the valence space to be completely degenerate in zeroth order. This is accomplished by introducing into hŽ of Eq. (3.2) a single averaged valence orbital energy ª´
v to replace the separate and generally different ´v. Such a method is perhaps more honestly called "forced degenerate perturbation theory". When Hv computations are designed to provide all low lying excitation energies simultaneously or to compare with semiempirical methods, the average valence orbital energy ª´v is taken as a equal weighted average of all valence orbital energies, but other choices are currently under investigation64. Extensive computations and comparisons with full CI calculations indicate that this procedure works well in third order, while there tends to be some overcorrecting in second order compared to third order and full CI for some model problems. Perhaps, other orbital energy averaging schemes could be developed to improve the practical convergence of Hv computations. (Some of these averaging methods correspond to infinite order diagram summations34). The ideal situation would be to have very accurate results from second order Hv calculations since the computational labor required is rather minimal.3.2. ILLUSTRATIONS OF RECENT AB INITIO Hv CALCULATIONS
The optimal way of testing new ab initio electronic structure methods is through comparisons with benchmark full CI computations because differences with full CI cannot be ascribed to inadequacies of the basis set as they may when comparisons are made with experiment. Some comparisons between full CI and the H
v method have been made for the CH¤ molecule62, for the insertion reaction of Be into H¤ at various geometries67, and most recently for the spectroscopic constants of the nitrogen molecule ground state64. These nontrivial comparisons attest to the capabilities of the Hv method, but the examples we present now are interesting cases in which large basis set Hv calculations for difficult systems are compared both to experiment and to other highly accurate correlated ab initio computations.The first example involves the computation of the pi-electron vertical excitation energies for the trans-butadiene molecule
65 which presents an interesting challenge in many respects. The low-lying pi-electron spectrum of trans-butadiene and other small conjugated molecules contains both valence-like and Rydberg states, as well as some states of mixed Rydberg-valence parentage. The accurate description of such a complicated spectrum is quite non-trivial because correlation in these three classes of states is both quantitatively and qualitatively different. Consequently, the ab initio method must adequately describe the differential correlation between these states of varying spatial character, a task whose difficulty is compounded by the highly open shell nature of some electronically excited pi-electron states.We begin discussion of the trans-butadiene H
v computations with a valence space resembling that of semiempirical pi-electron theory in containing four p¼ molecular orbitals. The primitive basis set contains 126 Gaussian functions and is constructed from a Huzinaga (4s3p/2s) basis augmented by (d/p) polarization functions and two diffuse sets of p-functions on all the carbon centers65. This basis set is of sufficient quality and size to warrant direct comparisons with experiment. The orbitals and orbital energies are defined as described already by the sequence of SCF computations in Eq. (3.1).This four orbital H
v computation is also useful in subsequently developing methods for testing the assumptions of pi-electron theories. Since semiempirical pi-electron methods with localized, transferable basis sets are designed, in principle, to provide only the valence-like states, it is only reasonable to expect the four-orbital valence space trans-butadiene Hv computations to represent these valence-like states. Before turning to these computations, we briefly note some significant differences between the calculations now discussed and those necessary for testing semiempirical theories. The optimized pi-electron molecular orbitals of Eq. (3.1) depart considerably from the localized, transferable basis of atomic p¼ valence orbitals implicit in semiempirical pi-electron theories. Nevertheless, the success of the ab initio Hv computations with these orbitals would demonstrate the practical validity inherent in the semiempirical assumption for using a minimal valence space, an assumption whose formal validity is already justified by our derivation of the effective valence shell Hamiltonian.The four-orbital valence space trans-butadiene H
v computations65 present a reasonably good description of the low-lying pi-electron valence and do not suffer from intruder state problems, even though many possible low-lying Rydberg states penetrate into the valence-like spectrum. The lowest two triplet 1£Bu and 1£Ag states excitation energies departing from experiment by only 0.13eV each. A larger error of 0.52eV appears for the 1¡Bu state which contains an admixture of some Rydberg character into a primarily valence-like state. The nearby Rydberg excited states are totally absent from the four-valence-orbital third order Hv calculations, despite the fact that they represent potential intruder states whose presence is widely believed50 as dooming to failure any multireference configuration perturbation formalism. However, the couplings between Rydberg and valence configurations are sufficiently small that they neither pose intruder state "problems" or permit entry of Rydberg states into the third order Hv calculations, even though we actually would like to describe these Rydberg states. Thus, these Hv computations once again produce a practical verification for the semiempirical assumption of using a minimal valence space.A more thorough ab initio description of the trans-butadiene pi-electron spectrum requires treating both the low-lying Rydberg and valence-like states. Thus, H
v computations have also been performed using six pi-electron valence orbitals65, four of valence-like character and two Rydberg pi-orbitals. The computed excitation energies compare well with both experiment and other highly correlated ab initio methods. The core and four valence-like orbitals are taken from the SCF sequence in Eq. (3.10), but step (4) of this sequence is replaced by the steps(4) [(core)(1¼
u)™(1¼g)¡(2¼u)º(2¼g)º](3¼u)¡, £Bu,(5) [(core)(1¼
u)™(1¼g)¡(2¼u)º(2¼g)º(3¼u)º](3¼g)¡, £Ag,(6) [(core)(1¼
u)™(1¼g)™(2¼u)º(2¼g)º(3¼u)º(3¼g)º], ¡Ag, (3.5)where the Rydberg molecular orbitals (one for each possible symmetry) are obtained as IVO's in steps (4) and (5) and the excited orbitals are computed in step (6). Table I presents the third order H
v computations of the trans-butadiene pi-electron excitation energies65 along with experimental values and the results of subsequent CASPT2 computations by Roos and coworkers. The CASPT2 method is also a perturbative approach, but it involves diagonalization and then perturbation as opposed to the perturb then diagonalize Hv method. More specifically, the CASPT2 trans-butadiene computations begin with a complete active space SCF computation with six active pi-orbitals. Then, single reference state second order perturbation computations are performed with each of the CASSCF wavefunctions separately. The Hv computations exhibit an average deviation from experiment of only 0.10eV, whereas the deviation for the CASPT2 method is the slightly larger 0.16eV. Table I also indicates the spatial character of the states (V denotes valence and R Rydberg) as well as the dimension of the primary space for each electronic state symmetry. The transition to the six-orbital valence space improves the Hv excitation energies of the valence-like 1£Bu and 1£Ag states by 0.11 and 0.10eV, respectively, but there is a considerable 0.43eV improvement in the energy of the 1¡Bu state,Table I: Third order Hv computations for trans-butadiene.
|
State |
Hv |
Experiment |
CASPT2 |
Dimension |
Type |
|
1£Bu |
3.20eV |
3.22eV |
3.20eV |
54 |
Valence |
|
1£Ag |
4.88 |
4.91 |
4.89 |
57 |
Valence |
|
1¡Bu |
6.01 |
5.92 |
6.23 |
48 |
.8V+.2R |
|
2¡Ag |
6.20 |
? |
6.27 |
57 |
Valence |
|
2¡Bu |
6.91 |
7.07 |
6.70 |
48 |
Rydberg |
|
3¡Ag |
7.17 |
7.4 |
7.47 |
57 |
Rydberg |
|
1™Bg |
8.72 |
9.07 |
35 |
Rydberg |
|
|
1™Au |
10.98 |
11.4 |
35 |
Rydberg |
which is of mixed Rydberg-valence character. In addition, the H
v computations now describe the 2¡Bu and 3¡Ag Rydberg states so well that the computations confirm the tentative assignment of the former and provide the assignment of the latter65. Thus, the six-valence orbital Hv calculations represent the most accurate to date for the trans-butadiene pi-electron vertical excitation energies. Table I also presents the 1¼u and 1¼g vertical ionization potentials, which emerge from the same Hv computation as the listed excitation energies. The only additional computational labor is associated with the almost trivial diagonalization of the Hv matrix for the ion states.Analogous H
v calculations have been completed for cyclo-butadiene and others are currently in progress for benzene and hexatriene. No experimental data are available for the cyclo-butadiene pi-electron states, so our computations for this molecule are designed to provide accurate predictions for guiding attempts to observe the elusive ultraviolet spectrum of this interesting molecule. The benzene Hv calculations use a 156 basis function correlation consistent basis, augmented with two sets of diffuse p-orbitals on each carbon. Preliminary calculations are available with a valence space of six valence-like orbitals. The average deviation from experimental pi-electron vertical excitation energies to eight valence-like states is only 0.28eV, only slightly worse than the corresponding 0.26eV from the CASPT2 method with a similar active space of six valence orbitals.The pi-electron H
v computations are important in several respects. Firstly, they demonstrate the high ab initio accuracy of the Hv method in computations with large basis sets and for highly nontrivial systems. Secondly, they provide numerical justification for the implicit semiempirical assumption that accurate electronic energies can emerge from an effective Hamiltonian containing a small number of valence orbitals. The accuracy of ab initio Hv calculations for pi-electron systems indicates that the Hv method can be applied to test common semiempirical assumptions concerning the description of pi-electron systems. Since these pi-electron systems represent the birthplace of modern semiempirical methods where many of the fundamental principles of semiempirical approaches have been developed, the pi-electron systems also provide a fertile testing grounds for other more specific assumptions of semiempirical methods that are present in the all-valence-electron methods. Before turning to these tests in the next section, however, we consider another illustration of recent Hv computations.One important application of electronic structure theories is to the computation of molecular potential energy surfaces and pathways of chemical reactions. The overwhelming majority of the most accurate potential surface computations, and especially those for open-shell systems, such as excited and transition states, rely on multireference configuration CI computations with appended Davidson corrections
7. These CI treatments are the method of choice because they provide the best uniformity of correlation treatment as a function of molecular geometry. Multireference coupled cluster methods, on the other hand, cannot yet treat the high asymptotic degeneracy necessary for describing the dissociation of the nitrogen molecule triple bond. Thus, we turn to the interesting problem of whether the size-extensive Hv method is capable of providing global potential energy surfaces. Prior computations for many potential energy curves of the diatomic molecules CH66, CH+ 66, Li¤, LiH, O¤59 O¤+ 59, and S¤60, recent ones for N¤64, and prior computations for triatomic hydrides63,67 attest to the ability of the Hv method to accurately generate a series of valence state potential curves simultaneously from a single computation of the third order Hv, provided the valence space is of the all-valence-electron type (i.e., eight valence orbitals for O¤, N¤, and S¤, but five for CH and LiH, etc.) While the eight valence orbital spaces for O¤, N¤, and S¤ already severely strain the quasidegeneracy constraints of the Hv method, as the size of the molecule grows further, the all-valence-electron valence space becomes for too large for use of the Hv method, and restricted valence spaces are necessary. Thus, we consider whether the Hv method can treat interesting global potential energy surfaces with less than the all-valence-electron valence space. The system chosen for this study is the methyl mercaptan (CH‹SH) molecule,, which is an important component in atmospheric pollution. The all-valence-electron valence space for CH‹SH contains twelve spatial orbitals and is probably at the current limits of feasibility for the Hv method. However, a reduced valence space is clearly highly desirable. Our interests lie primarily in the ground and lowest two excited A'' states which are pertinent to the photodissociation and polarized emission studies of Butler and coworkers76. The first excited A'' state of CH‹SH is a valence-like state, but the second A'' state is Rydberg, thereby making the computation of adequate potential surfaces highly non-trivial. Hence, our experience with conjugated hydrocarbons suggests the necessity for also having Rydberg orbitals in the valence space in order to properly treat the Rydberg state. This requirement again emphasizes the question of how well the Hv method fares with less than the Rydberg-extended all-electron valence space.The H
v computations for the CH‹SH potential surfaces77 use a 4-31G** (with 62 functions and diffuse s and p functions on carbon and sulfur) in order to permit comparisons with previous ab initio computations using the same basis. Hv calculations with a larger 102 function basis have also been performed at selected geometries to assess the basis set errors77. CASSCF calculations for the ground and low-lying excited states indicate that the 1¡A'' excited state wavefunction is obtained from the dominant ground state configuration by a 3a'' ü 11a' excitation, while the 2¡A'' CASSCF wavefunction is primarily a 3a'' ü 12a' excitation. This convenient situation suggests that the Hv computation might proceed with just a three orbital valence space containing the ground state occupied 3a'' and unoccupied 11a' and 12a' orbitals. However, these considerations of zeroth order wavefunctions do not assess the quasidegeneracy properties of the resultant valence space. The Hv method requires a reasonable energy gap both between the core and valence orbitals and between the valence and excited orbitals, as well as not too large a spread in valence orbital energies.
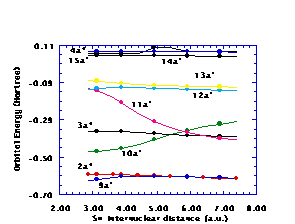
Figure 1. Selected CH‹SH orbital energies as functions of the SH distance
Figures 1 and 2 display the CH‹SH orbital energies as functions of the SH and CS distances
77, respectively, for several of the orbitals. Notice in both Figs. 1 and 2 that the 3a'' orbital energy crosses the ground state occupied 10a' orbital energy, suggesting that criteria of quasidegeneracy might require inclusion of the 10a' orbital in the Hv valence space to provide a valence space that is adequate over the whole (two-dimensional) range of geometries. The 10a' and 11a' orbital energies likewise cross at larger SH distances and at large CS distances. This crossing of orbital energies for orbitals of the same spatial symmetry is permissible because the 10a' and 11a' orbitals are eigenfunctions of different Fock operators, namely, the 10a' orbital is obtained from the ground state SCF wavefunction, while the 11a' orbital is an IVO from a 1¡A'' state computation. In a similar vein, the 11a' and 13a' orbitals become nearly degenerate for a CS distance of 3au, while these two orbitals are rather close in energy over the whole range of SH distances, suggesting the need for including the 13a' orbital in the Hv valence space. This leads to a five orbital valence space containing the ground state occupied 10a' and 3a'' orbitals as well as the ground state unoccupied (using IVO's) 11a', 12a', and 13a' orbitals. Thus, the 9a' and 2a'' orbitals are the highest orbitals in the Hv core, while the Hv excited space has the lowest orbitals as the 14a', 15a', and 4a'' orbitals. Notice that a reasonable gap exists between the core and valence orbital energies as well as between the valence and excited orbital energies. The spread in valence orbital energies, however, is sufficiently large that the Hv method must be applied to this five valence orbital space with averaged valence orbital energies. Thus, third order computations are necessary to include contributions from the difference between the actual orbital energies and the averaged values used in the zeroth order Hamiltonian.Known vertical excitation energies, bond energies, and ionization potentials serve as tests of the accuracy of the H
v computations. The vertical excitation energies to the 1¡A'' and 2¡A'' state are obtained with the 62 function production basis as 5.72 and 6.37eV, respectively, compared to the experimental values of 5.45 and 6.07eV. Extending the basis to 102 functions by uncontracting the 4-31G** basis and adding two sets of s and p diffuse functions on carbon and sulfur and two sets of diffuse functions on the hydrogen atoms leads to an improvement of the excitation energies to 5.50 and 5.92eV, respectively77. The 10a' and 3a'' orbital ionization potentials are computed with the 62 function basis as 12.21 and 9.69eV, respectively, compared to the experimental 12.08 and 9.44. Increasing the basis size to 102 functions yields the negligible changes to 12.22 and 9.66eV, respectively77. The absence of basis functions with higher angular momenta precludes the computation of highly accurate bond energies. The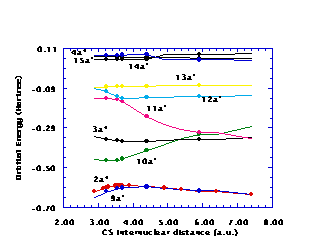
Figure 2. Selected CH‹SH orbital energies as functions of the CS distance
62 (102) function computations predict the CS and SH bond energies as 65.6 (62.4) and 82.4kcal/mole (81.5), while the experimental values are 72.6 and 86.1kcal/mole, respectively, yielding an accuracy comparable with that expected from the types of basis sets used.
Figures 3 and 4 depict cuts of the potential energy surfaces along the SH and CS distances, respectively. The potential surfaces correspond rather closely to the analogous surfaces for methanol, as they should. The full two-dimensional surfaces are being used in computations of the dynamics of photodissociation of CH‹SH.
4. Ab initio computations of correlated semiempirical-like integrals
Both the formal theory of section 2 and the ab initio H
v computations, described in section 3 and elsewhere, already explain certain fundamental aspects of semiempirical methods. First of all, the formal theory complely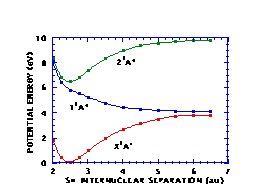
Figure 3. Cuts in CH‹SH potential energy surfaces along SH distance.
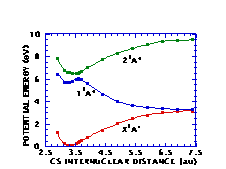
Figure 4. Cuts in CH‹SH potential energy surfaces along CS distance.
justifies the semiempirical assumption that it is, in principle, meaningful to represent the exact solutions of the molecular Schrÿodinger equation in terms of a valence electron only problem. This exact formal H
v theory also indicates that the simplest representation requires a complete valence shell CI calculation, although further approximations may be possible to reduce the computational labor from the full valence shell CI with a concomitant adjustment of the resultant approximate Hv matrix elements to compensate for the necessary approximations. The ab initio Hv computations, on the other hand, demonstrate the practical feasibility of using a minimal or smaller valence shell basis and performing state-of-the-art correlated computations based on the same Hv formulation.The formal theory and computations, however, also indicate the presence of several differences between the exact H
v and the semiempirical model Hamiltonians HMv in current usage. Foremost among these differences is the presence in the exact Hv of three, four, æææ electron effective interactions, which have no counterpart in semiempirical models. Since, as discussed below, the matrix elements of the three-body effective Hv interactions (either called Hv integrals or true parameters below) are rather large in some systems, the existence of these considerable non-classical many-body interactions already signals important departures between the true Hv and semiempirical model HMv. Thus, ab initio Hv computations are necessary to probe the structure of the exact Hv and to test the fundamental assumptions inherent in current model HMv. Our ultimate goal is the generation of systematic ab initio information that can be used to improve and extend semiempirical electronic structure methods.Perhaps the next most fundamental assumptions of semiempirical methods, beyond that inherent in the use of a minimal valence space, are those associated with the zero differential overlap approximation (ZDOA) and the assumption of transferability for the matrix elements of H
Mv within a localized atomic orbital basis. The ZDOA effectively enables elimination of all three and four-center repulsion integrals in HMv and even of some two and one-center repulsion integrals, depending on the degree of neglect of differential overlap. The ZDOA leads to considerable simplification of HMv over that from the valence shell matrix elements of the full Hamiltonian H, and this simplification is partially responsible for the ease and speed in applications of semiempirical methods. No less fundamental is the transferability assumption that the semiempirical HMv may be expressed in terms of a localized, transferable, molecule independent basis set with one-center and two-center matrix elements in this basis that depend, respectively, only on the atom and pair of atoms involved, independent of the remaining molecular environment.Because semiempirical methods derive their one-center matrix elements from atomic spectral data, the ab initio H
v test of the customary semiempirical one-center matrix elements merely requires performing Hv calculations for atoms with the Hv valence space chosen to correspond with that used in the semiempirical method52-57. More interesting questions arise in the computation of two-center integrals63,,,. First of all, a test of the transferability hypothesis requires use of a molecular valence space basis that is constructed from bases appropriate to the constituent atoms78. Thus, the molecular valence space must be constrained to be the union of the atomic valence spaces, with the molecular orbitals represented as linear combinations of the atomic valence orbitals. These "constrained" valence orbitals are naturally expected to provide a poorer initial description of HPP and therefore to require more Q-space correlation contributions for correcting this less than optimal starting point. Thus, the constrained orbital ab initio Hv computations are anticipated to display somewhat slower convergence than the "full" Hv calculations in which valence orbitals are variationally determined as described in section 3. In order that the Hv method be capable of providing insights into the transferability assumption and into forms for the true two-center parameters, we require that the constrained Hv computations be capable of providing a reasonably accurate description of the valence state energies. This, in turn, demands that the Hv method adequately correct for differences between the full and constrained valence orbitals. As already explained in section 3, the full ab initio Hv computations employ a single set of (variationally determined "full") valence orbitals, and the Hv method appears to describe perturbatively the influences associated with differences in optimal orbitals between different valence states. Thus, we may hope that the constrained Hv calculations likewise rectify some deficiencies of the constrained valence orbitals and thereby provide useful valence space energies and, more importantly, two-center true parameters. For brevity, the term constraining errors is used below to indicate the errors in computed valence state energies arising from use of constrained valence orbitals.If the constraining errors are indeed small, H
v computations for diatomic molecules suffice to determine the two-center true parameters and therefore complete the test of semiempirical assumptions concerning the bond length dependence of two-center integrals. However, calculations for diatomic molecules are inadequate for performing a thorough test of the transferability approximation. While the diatomic molecule examples78-80 do enable considering whether the one-center integrals remain the same in diatomics as they are in atoms, Hv computations for polyatomic molecules must provide the ultimate test of transferability of two-center integrals and the lack of dependence of the one and two-center true parameters (from atoms and diatomic molecules) on the molecular environment63. Thus, a quite extensive series of constrained ab initio Hv computations are necessary for probing the transferability and ZDOA assumptions of semiempirical methods. Until the recent explosion in available computational resources and the significant recent advancement in Hv method algorithms and computer codes, our progress with these fundamental questions has been limited to the consideration of atoms, a few diatomic molecules, one triatomic molecule, and trans-butadiene. However, with the recent advances in code performance and computational facilities, we have made enormous progress through a huge number of Hv calculations for several highly non-trivial conjugated pi-electron molecules65,70,71.This section continues with some examples from the H
v computations for atomic systems and the insights they provide into assumptions of semiempirical methods. For brevity, we omit a summary of the diatomic molecule Hv calculations of true two-center parameters78-80 and whether the one-center diatomic parameters are indeed the same as in the atom. Several general features of the diatomic molecule calculations are, however, also exhibited by the more extensive Hv treatments of the pi-electron systems, and the interested reader is referred to the original papers on the diatomic molecule computations78-80 for detailed tests of the bond length dependence of various two-center integrals. This section then closes with a brief description of the constrained Hv computations for the ab initio effective valence shell dipole operator,,, which provides dipole moments and transition dipole moments of all valence states. Constrained calculations of the effective dipole operator yield important insights into severe limitations of current semiempirical methods for molecular dipole properties.4.1. COMPUTATIONS OF ONE-CENTER H
V PARAMETERS FOR ATOMIC SYSTEMSA series of H
v computations have been performed for the atomic systems of C through F52, Si through P53, and Ti through Cr54, with the all-electron valence spaces of 2s2p, 3s3p, and 4s3d, respectively. We illustrate the basic conclusions by reference to the first row atoms and second order Hv calculations using unaveraged valence orbital energies and SCF orbitals for either the neutral atom or one of its ions. The particular SCF orbitals are taken as those from the ground state of C (neutral), N (+1 ion), O (+2 ion), F (+3 ion) as providing a compromise for describing all charge states52. The computations yield valence state excitation energies and valence orbital ionization potentials and electron affinity for the neutral atoms and all their ions simultaneously from a single computation of the Hv for the atom. These energies are obtained52 with average deviations from experiment of 0.32 (22), 0.31 (29), 0.38 (40), and 0.33eV (43) for the C, N, O, and F systems, respectively, where the numbers in parentheses indicate the numbers of energies involved in the comparison. Improved accuracy is currently possible with third order computations and larger basis sets than the 4s3p2d Slater bases used previously. (For instance, the average error in the oxygen computations is reduced by to 0.26eV in third order and should be diminished further upon expansion of the basis set.) Nevertheless, these 1980 computations are of sufficient accuracy to illustrate the salient physical points.The most important feature is the comparison of computed ab initio Hv one-center integrals with those of standard semiempirical methods as exemplified by MINDO/3. The following comparison considers the subset of Hv integrals that may also be uniquely represented as sums and differences of experimental energies for various neutral and ion states of the system since this also enables a comparison of Hv integrals directly with experiment
56. For instance, the ionization potentials of the (1s)™2s and (1s™)2p states provide the exact experimental values of the one-electron Hv integrals âs|sê … â2s|HŽv|2sê and âx|xê … â2px|HŽv|2pxê, respectively. Likewise, the two-valence-electron state energy differences {E[¡D(p™)] ± E[£P(p™)]}/2 yield (upper sign) the one-center repulsion integral âxy|xyê … â2px2py|HŽ¤v|2px2pyê and (lower sign) the one-center exchange integral âxy|yxê, respectively. Thus, Table II compares ab initio52 Hv one-center, one-electron and selected one-center, two-electron integrals with experiment and with MINDO/3 values87.Notice that the H
v integrals are in good agreement with experiment. The differences arise from incomplete inclusion of correlation contributions by virtue of the use of a second order perturbation truncation and a limited basis set. The MINDO/3 integrals, on the other hand, are vastly different from the Hv or experimental values! The MINDO/3 one-center, one-electronTable II. Comparison of H
v, experiment, and MINDO/3 integrals.|
C |
N |
O |
F |
|||||||||
|
Integral |
Hv |
Expt |
M/3 |
Hv |
Expt |
M/3 |
Hv |
Expt |
M/3 |
Hv |
Expt |
M/3 |
|
-âs|sê |
64.70 |
64.50 |
51.79 |
98.24 |
97.90 |
66.06 |
138.5 |
138.1 |
91.73 |
185.4 |
185.2 |
129.9 |
|
-âx|xê |
57.33 |
56.49 |
39.18 |
88.32 |
87.90 |
56.40 |
126.1 |
126.1 |
78.80 |
171.0 |
171.2 |
105.8 |
|
âsx|sxê |
19.13 |
18.20 |
11.47 |
23.51 |
22.69 |
12.66 |
27.78 |
27.16 |
14.48 |
32.13 |
31.63 |
17.25 |
|
âsx|xsê |
3.41 |
3.10 |
2.43 |
4.20 |
3.93 |
3.14 |
4.97 |
4.72 |
3.94 |
5.75 |
5.56 |
4.83 |
|
âxy|xyê |
19.36 |
18.17 |
9.84 |
23.81 |
23.02 |
11.59 |
28.20 |
27.86 |
12.98 |
32.86 |
32.66 |
14.91 |
|
âxy|yxê |
0.68 |
0.52 |
0.62 |
0.95 |
0.82 |
0.70 |
1.21 |
1.10 |
0.77 |
1.50 |
1.41 |
0.90 |
integrals are 30-55eV more positive than Hv or experiment, while the MINDO/3 one-center, two-electron repulsion integrals are considerably more positive (by 8-17eV) than those from H
v or experiment. The Hv and experimental repulsion integrals âsx|sxê and âxy|xyê are, in fact, considerably larger than the neutral atom "bare," or theoretical SCF, integrals by several electron volts. Thus, the ab initio true empirical Hv departs severely from the assumptions of standard semiempirical methods. Consequently, the semiempirical methods are either grossly in error or a more fundamental explanation exists.The second order H
v, on the other hand, also contains three-electron interactions, which are formally absent from semiempirical methods. Several of the three-electron Hv integrals may likewise be expressed exactly in terms of differences of ion energy levels56. Thus, these experimental three-electron integrals are known to accuracies of roughly a cmÄ¡. Table III presents a comparison of the experimental three-electron Hv integrals with those computed from the second order Hv computations52 using the convenient notation in which, for instance âsxy|sxyê … â2s2px2py|HŽ¤‹v|[2s2px2py-2py2px2s]ê. (The tabulated three-body Hv integrals contain a direct and exchange contribution because the existence of only two possible spins for the electron implies the physical impossibility of separating the direct and exchange contributions. However, it is possible mathematically to define a set of spin-independent three-body integrals, but this separation is unnecessary here.)Table III. Comparison of some three-body Hv integrals with experiment.
|
C |
N |
O |
F |
|||||
|
Integral |
Hv |
Expt |
Hv |
Expt |
Hv |
Expt |
Hv |
Expt |
|
âsxy|sxyê |
-2.69 |
-1.87 |
-2.45 |
-1.95 |
-2.23 |
-1.97 |
-2.13 |
-1.90 |
|
âsxy|syxê |
0.02 |
-0.12 |
0.05 |
0.06 |
0.07 |
0.08 |
0.07 |
0.06 |
|
âsxy|xsyê |
-0.44 |
0.06 |
-0.38 |
-0.27 |
-0.33 |
-0.21 |
-0.29 |
-0.23 |
|
âxyz|xyzê |
-3.59 |
-2.97 |
-3.32 |
-2.85 |
-3.02 |
-2.87 |
-2.94 |
-2.79 |
|
âxyz|xzyê |
-0.17 |
-0.15 |
-0.15 |
-0.13 |
-0.12 |
-0.13 |
-0.13 |
Notice the huge magnitudes, for instance, of âxyz|xyzê, whose experimental values of roughly 3eV are fairly independent of atomic number (within a row of the periodic table) and are in reasonable agreement with the second order H
v computations. With hindsight, this large magnitude is not so surprising. The lowest order contributions to the three-body Hv interactions involve single orbital excitations [see Eq. (2.12)] and represent orbital polarization contributions which correct for differences in the orbitals that are "optimal" for different valence states. The other large three-body integral âsxy|sxyê in Table III is likewise quite independent of atomic number and is in decent agreement with the Hv calculations. Several other computed three-body integrals are in the range of 2-4eV for the first row atoms carbon through fluorine. The presence of these large three-body parameters contrasts sharply with semiempirical methods which do not contain explicit three-body interactions.Without the formal H
v theory, it would have been impossible to deduce the presence of large three-body integrals. Some reflection suggests that the semiempirical methods must somehow be averaging55 these large three-electron integrals into their one and two-body integrals similar to the general spirit in which a one-electron Fock or MCSCF Fock operator contains an average of two-body interactions. A particular illustrative (but not necessarily optimal) averaging scheme has been applied to the carbon atom ab initio Hv parameters55 and produces averaged integrals close in magnitude to MINDO/3 values. For instance, the averaged Hv (and corresponding MINDO/3) integrals âs|sê, âx|xê, âss|ssê, and âsx|sxê are -50.28 (-51.79), -40.83 (-39.18), 13.59 (12.23), and 10.49eV (11.47), respectively. While not perfect agreement, the correspondence is enormously closer than that between the unaveraged Hv parameters and MINDO/3 integrals. This similarity between these two sets of integrals justifies the above assertion that semiempirical methods are effectively averaging the influence of the three and higher-body Hv integrals into the semiempirical parameters. (Third order Hv computations indicate that four-body integrals are roughly an order of magnitude smaller than the three-body parameters86.)It would appear that the semiempirical methods are attempting to have their cake and eat it. These methods implicitly average the large three-body H
v interactions into their one and two-electron parameters, and they expect that these averaged parameters are transferable between different molecules. The following analysis of this implicit averaging provides some general insights into the ranges of validity for conventional types of semiempirical methods: Just as portions of one-electron Fock operators are somewhat transferable if local environments are very nearly identical, a particular averaging scheme for three-electron integrals may be reasonable for systems with similar (but a wider range of) electronic structures. Organic molecules have carbon, oxygen, nitrogen, etc., within fairly narrow ranges of effective charges but with a range of hybridizations about the central carbon atom. Thus, it is possible that a suitable three-body averaging scheme exists and applies well to this range of local environments. This possibility accords with the development of fairly accurate all-valence electron semiempirical methods for these systems. Transition metal atoms, on the other hand, occur in chemical compounds with a very wide range of formal charges and with high and low spin states. Third order Hv computations for Ti through Cr54 obtain a large number of three-body integrals lying in the range of 2-3eV. We believe it rather unlikely that there exists a three-body averaging scheme for the transition metal which is adequate with all possible formal charges and spin couplings. This conjecture is in conformity with the absence of a semiempirical method for transition metals in which there is a common set of parameters for all charge and spin states of a given transition metal atom.Calculations have been made of the bond length dependence of two-center, one and two-body Hv integrals for diatomic molecules
78-80. Some of these bond length dependences have identical forms as those invoked by semiempirical methods, but only after correlation contributions are included. Other two-center integrals have a slightly different form from the traditional semiempirical parameterizations, while a few integrals depart considerably in their bond length dependence. However, the all-valence electron Hv treatments produce large three-body parameters, which should really be averaged into the one and two-body integrals for proper comparison of the averaged Hv with their semiempirical counterparts. Thus, additional work is of interest on developing "optimal" three-body averaging schemes. We now turn to tests of the fundamental semiempirical assumptions of transferability and zero differential overlap approximation that are common to all semiempirical methods.4.2. AB INITIO COMPUTATION OF PARAMETERS IN PI-ELECTRON METHODS
Because of the high accuracy afforded by full ab initio H
v computations for pi-electron systems, it is quite natural to apply the more approximate constrained Hv computations to pi-electron systems in order to test and refine the assumptions of semiempirical pi-electron methods, such as that of Pariser-Parr-Pople (PPP) theory. The pi-electron systems provide an ideal system for beginning tests of the transferability and zero differential overlap approximations, which are common to the all-valence electron semiempirical methods. Thus, understanding and advancements made with the pi-electron systems have immediate ramifications for the more complicated all-valence electron systems. Pi-electron methods are still widely used22,24, for studying the properties of conducting and nonlinear polymers23 and for treating the electronic structure of complex biological molecules. Consequently, improvements in pi-electron methods have direct applicability to these interesting systems. In addition, virtually all electronic structure theories of solids are semiempirical in nature. For example, the widely used Hubbard-type models for solids have the same formal structure as PPP theory. Thus, fundamental understanding gleaned from studying pi-electron systems suggests possible improvements with semiempirical models for the electronic structure of solids.Some ideal characteristics of the pi-electron systems for performing these tests include the fact that there are only a small number of pi-orbitals, and the symmetries are generally high. Consequently, the number of ab initio Hv parameters for analysis is kept to a minimum. Another significant feature of the pi-electron H
v emerges because the three-body parameters are considerably smaller than in the all-electron example of atomic one-center integrals described in subsection 4.1. The largest three-body Hv parameters are generally the diagonal one-center integrals, but the pi-electron Hamiltonians have just a single pi-electron orbital per main atom center (carbon atoms in the examples below.) Thus, the largest three-electron integrals for the pi-electron systems are the two-center, diagonal interactions, which are considerably smaller than the approximate 4eV magnitudes found for first row atoms in the all-valence electron Hv. Old, smaller basis set trans-butadiene Hv computations with a non-transferable set of pi-orbitals yield the largest three-body integrals as 0.74eV. Hence, the test of semiempirical assumptions for pi-electron systems presents the least complications from the necessity for averaging the three-body parameters into the one and two-electron integrals.Full, ab initio H
v computations, such as those described in section 3, use a set of variationally determined orbitals. The construction of these orbitals represents an attempt to "optimize" the first order description HPP that is provided by the core and valence orbitals. However, these "optimal" variational valence orbitals exhibit a strong molecule dependence. The semiempirical methods, on the other hand, assume the existence of a universal, transferable, molecule independent basis set of valence orbitals which depend solely on the constituent atoms and which are to be used for all valence states of both the neutral and ion states for all molecular systems. Thus, the comparison of ab initio Hv calculations with semiempirical methods requires that we perform more approximate Hv computations in which the constrained valence orbitals are constructed from such a transferable basis set. These constrained valence orbitals provide less than an optimal first order description from HPP, and consequently, they must also slow the convergence of the Hv perturbation expansion. Thus, it is necessary first to test the ability of the Hv method in describing the pi-electron spectrum with this constrained valence space. While higher order computations with constrained orbitals might be of very high accuracy, our computations are limited to third order, and therefore we must consider the "practical" convergence of the third order constrained Hv calculations for the pi-electron systems.The construction of constrained valence orbitals is quite straightforward for the pi-electron systems. The transferable, localized basis contributes one p
¼-like valence orbital p¼(i) on the ith carbon atom center, and these p¼ basis functions are naturally nonorthogonal. Molecular orbitals ƒåmo are then formed as linear combinations of these individual p¼ orbitals,,
ƒ= C
i,åp¼(i), (4.1)
where symmetry in many systems dictates all or a portion of the expansion coefficients {C
i,å}. Since the core orbitals are not specified in semiempirical methods, our constrained orbital Hv computations employ a variationally optimized set of core and excited orbitals93, determined according to the same sequential set of SCF calculations as in Eq. (3.5), except for the constraint in Eq. (4.1) upon the construction of the valence orbitals. Constrained Hv computations for pi-electron systems have so far considered only the simplest choice for the transferable pi-orbitals p¼(i), namely, carbon atom SCF p¼ orbitals92,93, although other possibilities should be tested in the future. Notice that the resultant molecular orbitals, therefore, omit important polarization components, for instance, those that move some pi-electron density onto the hydrogens as is present in optimal (called "full") Hv and other ab initio calculations. The Hv computations described in section 3 indicate the ability of the Hv method to compensate for the state dependence of valence orbitals appearing in traditional wavefunction methods, but the constraints in Eq. (4.1) on the valence orbitals are quite a bit more severe.Differences (called constraining errors), of course, appear between "full" and constrained H
v computations for the pi-electron systems. The constrained Hv calculations poorly represent excitation energies to valence states of primary Rydberg character83, but this is as anticipated since the traditional pi-electron Hamiltonian is represented in terms of valence-like pi-orbitals and should not generate a satisfactory description of the low-lying Rydberg states. Hence, the analysis of constraining errors is limited to states of only valence-like parentage. The possibility exists that higher order Hv computations could converge well to the excitation energies (but not the spatial extent) of states with mixed Rydberg-valence parentage, such as the 1¡Bu state in trans-butadiene which has approximately 20% Rydberg character. However, the third order constrained Hv calculations appear unable to represent such mixed character states well. (For instance, the constraining error for the 1¡Bu state is a considerable -0.69eV.) Thus, constrained Hv computations are useful in testing basic assumptions of semiempirical pi-electron methods if the constraining errors are tolerable for the low-lying valence-like pi-electron states.Table IV summarizes the constraining errors obtained for trans-butadiene with a ccPVDZ basis augmented with two Rydberg carbon p functions
93. The constraining errors (difference between full and constrained calculation) for the ground state energy, excitation energies to three low-lying valence-like states, and the two lowest ionization potentials in Table IV are an average of 0.23eV. The three-body errors in Table IV designate the difference between full Hv computations with and without the three- and four-body interactions. The average three-body error in Table IV is 0.21eV. The combined error designates the difference between full Hv computations and constrained calculations with omitted three- and four-body interactions. The combined average error of 0.16eV indicates that the constraining and three-body errors are non-additive, but, more importantly, the small magnitude of the combined error demonstrates that a reasonably good approximation is provided by the approximate constrained Hv computations with only one and two-body effective interactions. If, on the other hand, the combined error is determined instead with respect to the experimental energies (available in Table I), then the combined error shrinks to a mere 0.08eV. Similar computations for several other conjugated hydrocarbons yield combined errors with respect to experiment that are comparable to those from the full Hv calculations. Hence, we have the remarkable occurrence that the approximate, constrained calculations with neglected three- and four-body interactions yield highly accurate descriptions of the valence-like states of all conjugated hydrocarbons using a single universal basis set of p¼ valence orbitals for all these systems! Consequently, we can certainly use the constrained Hv one- and two-body interactions to test the basic approximations invoked by semiempirical methods. (Additional universal valence shell basis set computations are desirable for larger systems to determine if the combined error with respect to experiment remains so small.Table IV. Constraining errors for low-lying pi-electron states of trans-butadiene.
|
State |
Constraining Error |
3-body Error |
Combined Error |
Type |
|
X¡Ag |
0.13 |
-0.19 |
-0.24 |
Valence |
|
1£Ag |
-0.15 |
-0.17 |
-0.19 |
Valence |
|
1£Bu |
-0.16 |
-0.16 |
-0.04 |
Valence |
|
2¡Ag |
-0.47 |
-0.48 |
-0.17 |
Valence |
|
1™Bg |
-0.22 |
0.09 |
0.20 |
Valence |
|
1™Au |
-0.26 |
0.17 |
0.12 |
Valence |
While it may be possible to reduce the constraining and three-body errors by investigating methods for "optimizing" the localized, transferable, atomic p
¼ basis and for averaging the three-body parameters into the one- and two-body parameters, respectively, the errors with the current calculations are sufficiently tolerable for using these constrained computations to assess for pi-electron systems the validity of the ZDOA and the transferability assumptions which are common to all semiempirical methods. We, therefore, begin by examining the repulsion integrals neglected by the ZDOA.Because Lÿowdin orthogonalization is generally invoked as providing the justification for the ZDOA, the ZDOA neglected two-electron constrained Hv parameters are presented in the Lÿowdin carbon atom p¼ basis using the conventional notation âij|klê … âp
¼(i)(1)p¼(j)(2)|H12v|p ¼(k)(1)p¼(l)(2)ê. Theoretical (or "bare") integrals are denoted with a subscript zero. The largest bare integrals among the ZDOA neglected ones are the nearest neighbor two-center exchange â12|21ê‚, the two-electron hybrid integral â11|22ê‚, and the two-electron contribution â12|11ê‚ to the resonance integral. The latter two-bare integrals are identical but generally have different correlation contributions. The illustrations provided below consider examples drawn from ethylene, trans-butadiene, cyclobutadiene, benzene, and preliminary computations for trans-trans-hexatriene. In order to test parameter transferability, comparisons of Hv parameters are made using computations in which the geometries are taken as similar as possible. Thus, for instance, the ethylene geometry is distorted slightly to have the same double bond length and HCH angle as in trans-butadiene93,94. (The distorted geometry ethylene Hv parameters are rather close to those evaluated at the ethylene ground state geometry.) Likewise, computations for square cyclobutadiene use the same CC bond length as either trans-butadiene of benzene.The inclusion of correlation contributions is important in providing the true justification of the ZDOA. The bare â12|21ê‚ = â11|22ê‚ for distorted ethylene are 0.126eV, but upon introducing correlation, the H
v parameters are reduced to 0.001 and -0.007eV, respectively94. These truly negligible values are likewise obtained for all other pi-electron systems studied to date. For example, they become 0.021 and -0.013eV for trans-butadiene. However, correlation converts the â12|11ê parameter from the bare value of -0.277 to the rather non-negligible 0.281eV. Again, constrained Hv computations for other linear pi-electron systems yield significant â12|11ê, e.g., 0.235eV in trans-butadiene; however, the somewhat smaller -0.134 and -0.051eV are obtained for the cyclic systems of (square) cyclo-butadiene and benzene (both with the benzene CC bond length), respectively. More computations are necessary to ascertain whether this difference between linear and cyclic systems is significant, but the available results suggest that an improved pi-electron theory should consider inclusion of the two-electron contribution â12|11ê to the nearest neighbor resonance integral.The non-negligible two-electron parameter â12|11ê is quite interesting. Iwata and Freed
19 have shown that this parameter (along with the three-body analogs such as â112|111ê) contribute to a breakdown of the pairing theorem for alternant hydrocarbons, leading, for instance to the observed asymmetry between spectra for anions and cations. More recently, Hirsh has argued for the necessity of retaining the analogous nearest neighbor â12|11ê integral in theoretical description for the electronic structure of high temperature superconductors18. Constrained Hv computations should be performed to evaluate this (and other) correlated integrals for the copper oxide systems.As the atomic centers become more removed, both the bare ZDOA neglected repulsion integrals and their correlation contributions diminish considerably. Thus, the trans-butadiene bare Lÿowdin basis â13|31ê and â14|41ê exchange integrals of 0.011 and 0.001eV, respectively, are transformed into the correlated third order H
v integrals of 0.003 and 0.0001eV94. While correlation again considerably reduces these integrals, their bare values are already quite negligible. Similar trends are obtained for the two-center hybrid integrals â11|33ê and â11|44ê, while the Hv two-electron resonance integral â11|13ê of trans-butadiene is roughly -0.1eV and may therefore warrant retention in an improved pi-electron method.The bare counterparts of the one-electron, one-center integrals å
i = âi|iê … âp¼(i)(1)|H1v|p ¼(i)(1)ê are understood to depend on local geometry since electrons on the ith atomic center experience fields due to the surrounding atoms. Thus, the Hv åŽ differs from å¤ for trans-butadiene (by roughly 4eV) as well as for other inequivalent atomic centers, and the only potential transferability is associated with the correlation contributions to å which range between 1-3eV. Trans-butadiene and distorted ethylene have the correlation portion of åŽ transferable (i.e., equal) to within a remarkable 0.012eV out of the total correlation contribution of 1.44eV. However, this is a rather unusual case in which the geometries are very similar. The less similar cases of benzene at its equilibrium geometry and square cyclobutadiene (with the same CC bond length as in benzene) yield correlation contributions to å that differ by a substantial 0.6eV71. Thus, a rather systematic study is necessary to elucidate the nontrivial but significant geometry dependence of correlation contributions to the Hv å parameters.
Fortunately, the correlation contributions to the å parameter exhibit the worst transferability. The other one-electron pi-electron integrals are the resonance integrals †
ij … âp¼(i)(1)|H1v|p ¼(j)(1)ê and are best analyzed again in a Lÿowdin orthogonalized basis set. Again using as close as possible to a common geometry, the Hv †Ž¤ for ethylene, trans-butadiene, and trans-trans-hexatriene (preliminary) are -3.43, -3.34, and -3.15eV, respectively, while the single bond †¤‹ for the latter two molecules are -2.57 and -2.37eV, respectively94. The ZDOA neglected †Ž‹ and †Ž› in trans-butadiene are 0.24 and 0.06eV, respectively, thereby justifying the neglect of †Ž› but not of †Ž‹. Computations of †Ž‹ for cyclobutadiene yield 0.24eV, while those for benzene (at its equilibrium geometry) obtain 0.29eV, further supporting the necessity for retention of this customarily neglected pi-electron integral.The one-center, two-electron repulsion integrals ©
ii … âp¼(i)(1)p¼(i)(2)|H12v|p ¼(i)(1)p¼(i)(2)ê contain the largest correlation contributions (roughly 4eV), but display comparable transferability to the †ij and far superior transferability to the åi. The bare integrals ©iiº are exactly transferable when evaluated with the non-orthogonal localized pi-orbitals, so our discussion of repulsion integrals is conveniently presented using this basis. The transferability of ©ŽŽ between ethylene, trans-butadiene, and trans-trans hexatriene is quite remarkable, with values of 11.78, 11.83, and 11.83eV, respectively. The computed ©¤¤ differs slightly from ©ŽŽ because correlating electrons on these two atomic centers experience different environments. The difference |©ŽŽ-©¤¤| in trans-butadiene is the rather small 0.02eV but grows slightly to 0.14eV in trans-trans-hexatriene. The double bond ©Ž¤ Hv integrals are 7.47, 7.70, and 7.55eV, respectively, for ethylene, trans-butadiene, and trans-trans-hexatriene, while the single bond ©¤‹ for the latter two molecules are 7.34 and 7.22eV, respectively. Since it is doubtful that our constrained, third order Hv calculations for the ©ij are accurate to better than 0.1eV, these results provide strong support for the transferability of the correlated Hv repulsion integrals.The constrained H
v computations for pi-electron systems provide deep insights into the transferability and ZDOA assumptions that are common to all semiempirical methods. Firstly, the computations focus on the correlated parameters and not on the irrelevant theoretical integrals customarily analyzed in developing semiempirical parameterization schemes. Correlation is found to diminish the magnitudes of all of the ZDOA discarded parameters to a truly negligible magnitude, except for the two-electron contribution to resonance integrals and next nearest neighbor resonance integrals, which are computed with values in the range of 0.2-0.3eV (depending on system and parameter) and which therefore merit retention in improved pi-electron methods. Rather good transferabilities are found for resonance and repulsion integrals, with the correlation contributions to the one-center, one-electron å parameters displaying the greatest sensitivity to local environment. Further extensive Hv computations are necessary to map out such interesting behaviors as the bond length and environment dependence of the true Hv parameters, as well as to introduce improvements from optimizing the atomic p¼ orbitals and from averaging the influence of neglected three-body and other neglected small Hv parameters. Nevertheless, the constrained Hv computations to date provide excellent justifications for some, but not all, assumptions of semiempirical pi-electron methods, and, more importantly, these computations provide significant information into how correlation contributes to individual parameters. The latter insight is buttressed by a computational approach that enables evaluation of the individual parameters to determine a set of approximations and parameters for developing improved semiempirical methods.4.3. AB INITIO COMPUTATIONS OF THE EFFECTIVE DIPOLE OPERATOR: COMPARISONS WITH SEMIEMPIRICAL METHODS
Just as section 2 demonstrates how it is possible to construct an effective valence shell Hamiltonian that acts only on the space spanned by a set of valence orbitals, a straightforward generalization produces effective operators for properties other than the energy. For instance, if A is a Hermitian operator corresponding to an observable and if ˆ
iv is an eigenfunction of Hv corresponding the exact eigenfunction ˆi of the full Hamiltonian H, we may likewise derive an effective operator Av such thatâˆ
i|A|ˆjê = âˆ|Av|ˆ ê. (4.2)Equation (4.2) implies that the exact expectation values (for i=j) and exact transition matrix elements (for i‚j) of the full operator A may alternatively be evaluated as matrix elements of the valence shell operator A
v using the eigenfunctions of the effective valence shell Hamiltonian. (Both the exact and Hv eigenfunctions are taken as normalized to unity.61) Consequently, semiempirical treatments of properties other than energies are implicitly attempting to approximate the structure of the true Av and its valence space matrix elements.Numerical applications to date of the effective operator method have been limited to the computation of the effective valence shell dipole operator µ
v whose evaluation provides dipole moments, transition dipole moments, oscillator strengths, radiative lifetimes, etc.83-85. The computations consider the leading order correlation corrections and formally resemble83 a portion of the second order Hv calculations. Recent work has finally provided the rather non-trivial derivation of the next order terms. Particular ab initio applications of the µv method consider first row diatomic hydrides. Calculated dipole properties for these systems compare rather favorable to those from experiment and from highly correlated ab initio methods with basis sets of similar quality. We omit details of the computed ab initio dipole properties and instead focus on comparisons with semiempirical methods.The leading order correlated effective valence shell dipole operator µ
v contains a core contribution µc as well as both one- and two-body operators. The µv computations demonstrate that the two-body matrix elements are non-negligible and must be retained for ab initio accuracy. Hence, semiempirical dipole theories should again implicitly average these two-body dipole contributions into the retained one-body dipole operators. Constrained µv calculations for the CH molecule (and for CH+) agree well with full computations over a range of internuclear separations that includes the ground state equilibrium internuclear separation. Thus, we compare the constrained one-electron µv matrix elements with their semiempirical counterparts.Taking the carbon atom at the origin of the coordinate system, the z-axis along the molecular bond, and the internuclear separation as 2.1au, several ab initio constrained µ
v matrix elements qualitatively resemble those in semiempirical methods. For example, the carbon 2s and 2p¼ diagonal matrix elements of the z-component zv are 0.016 and 0.004au, respectively, in good agreement with the semiempirical treatment of these integrals as vanishing. Likewise, the ab initio off-diagonal â2s|zv|2pßê matrix element on carbon is 0.934, while the corresponding semiempirical integral is the similar 0.888au. There are, however, some major differences: For instance, the two-center integral â1sH| zv|2pßê is obtained from the µv computations as 0.203au, but the semiempirical treatment (with two-center integrals retained) yields a considerably different 1.028au. Similarly, the semiempirical vanishing â2pß| zv|2pßê contrasts sharply with the ab initio computed 0.771au.To understand the origins of this sharp discrepancy between the ab initio and semiempirical dipole matrix elements, it is useful to recall the customary point charge model for computing the semiempirical matrix elements. Each atom is considered as a point charge with the charge densities computed from the population densities that follow from the semiempirical wavefunction. The diagonal dipole matrix elements are obtained from the atomic charge densities, while the off-diagonal matrix elements are computed using single Slater functions. Thus, the point charge model represents the use of an approximation to the theoretical dipole matrix elements. As noted above and in the literature
3, an important component in the success of semiempirical methods for electronic energies lies in the empirical "adjustment" of valence shell matrix elements to include correlation contributions. However, these correlation contributions are completely omitted from the semiempirical dipole matrix elements! This observation already raises serious concern. Semiempirical dipole moments are notoriously poor for small molecules, suggesting that the correlation contributions are not negligible.Further analysis of the constrained µ
v computations provides insights into some deficiencies of the current semiempirical dipole treatment and into methods for its improvement. The largest discrepancy between µv matrix elements and those of the point charge model emerge for matrix elements containing either the bonding carbon 2pß or hydrogen 1s orbitals (or both). These two orbitals in full ab initio SCF computations have polarization contributions that somewhat affect computed energies but have dramatic influences on dipole matrix elements. The semiempirical point charge model dipole matrix elements completely neglect these important polarization contributions. On the other hand, polarization corrections enter into the constrained µv calculations through the perturbation corrections. Thus, it is not surprising that the greatest discrepancies between semiempirical and constrained µv matrix elements emerge for the most polarized valence shell orbitals.The ab initio effective dipole operator calculations represent only an initial application of the effective operator approach, but they strongly suggest that an improved semiempirical dipole method must, at least, include corrections due to orbital polarization. Additional contributions from true "correlation" processes would also be desirable. The appropriate forms might be deduced by trial and error parametrizations using polarized SCF orbitals, but extensive ab initio µ
v computations should provide an alternative route to generate a data base from which to discern general trends.5. Acknowledgments
This research is supported, in part, by NSF Grant CHE93-07489. I am grateful to the many talented graduate students and postdocs who have contributed to this research. Thanks go to Chuck Martin for his comments on the manuscript.